몇 년 전 처음 광학 관련 프로젝트를 맡았을 때, 저는 ‘각도(angle)’라는 단어를 너무 가볍게 생각했었습니다. 처음에는 각도와 입체각의 개념을 혼동하며 사용하였습니다.
렌즈의 시야각(FOV), 조명의 조사각(beam angle), 센서의 감지 범위—all 그저 ‘몇 도(°)’라는 숫자로만 인식했죠.
그런데 막상 조명 시뮬레이션을 하다 보니, 단순한 평면 각도로는 공간상의 빛의 분포나 시야 범위를 제대로 표현할 수 없다는 걸 깨달았습니다.
이때 처음 마주한 개념이 바로 **입체각(Solid Angle)**이었습니다.
🧭 입체각(Solid Angle)이란?
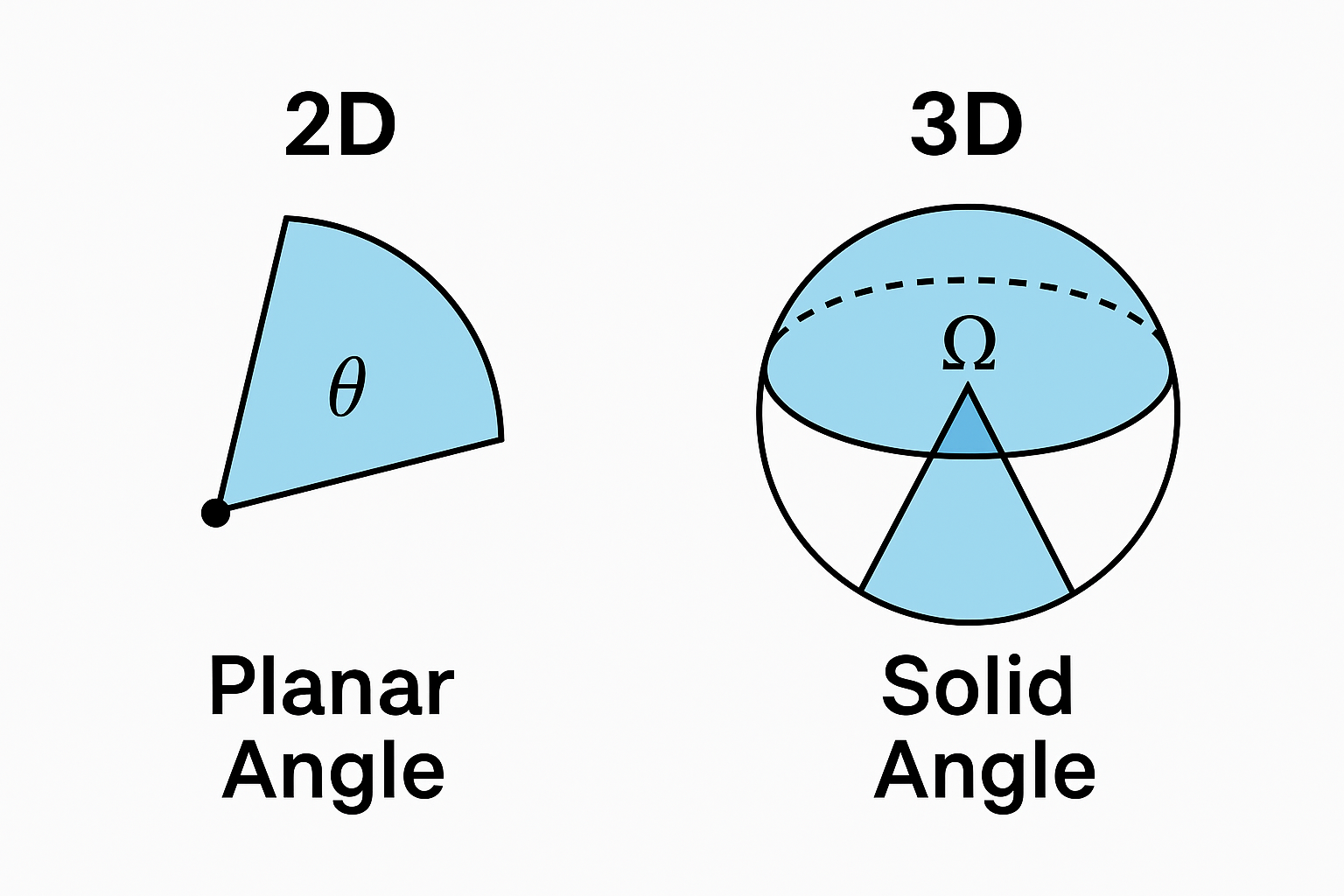
우리가 평소 사용하는 각도는 대부분 2차원 평면상의 **평면각(Planar Angle)**입니다.
예를 들어, 시계의 바늘이 이루는 각도나 삼각형의 내각, 카메라의 수평 화각은 모두 평면 위에서의 각도를 의미합니다.
하지만 현실의 세상은 3차원 공간이죠.
빛, 영상, 센서 데이터는 모두 공간적으로 확산되고, **입체각(Solid Angle)**은 바로 이런 3차원 공간에서의 “시야 범위”를 표현하는 개념입니다.
간단히 말해,
입체각이란 구의 중심에서 볼 때, 구면 위의 특정 면적이 차지하는 공간적 각도입니다.
🔹 비유로 이해하는 입체각
평면에서는 원의 중심에서 부채꼴 모양의 면적이 ‘각도’를 의미합니다.
입체에서는 구의 중심에서 뻗은 원뿔 모양, 혹은 오렌지 조각 같은 모양이 입체각을 나타냅니다.
즉, 평면에서의 각도가 ‘선’으로 면적을 나눈 개념이라면,
입체각은 ‘면’을 기준으로 구면 위의 공간을 나누는 개념입니다.
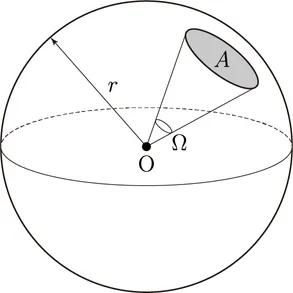
🔸 단위: 스테라디안(Steradian)
- 평면각 → 라디안(rad)
- 입체각 → 스테라디안(sr)
전체 구면(구 전체)의 입체각은 다음과 같습니다.
4π sr ≈ 12.57 sr
즉, 지구 전체를 한 점(관찰자)에서 바라보는 시야 범위가 약 12.57스테라디안이라는 뜻입니다.
| 구분 | 입체각(sr) | 비고 |
|---|---|---|
| 전체 구면 | 4π ≈ 12.57 | 전방위 시야 |
| 반구 | 2π ≈ 6.28 | 180° × 180° |
| 90° × 90° | 약 1.0 | 정사각 시야 |
| 120° × 120° | 약 2.37 | 와이드 렌즈 |
| 150° × 150° | 약 4.49 | 초광각 렌즈 |
| 180° × 180° | 6.28 | 반구 시야 |
| 210° × 210° | 7.85 | 광역 시야 |
| 240° × 240° | 9.27 | 거의 전방위 |
| 360° × 180° | 12.57 | 전구면 시야 |
🧮 입체각 계산 공식
가장 일반적으로 사용되는 입체각 계산식은 다음과 같습니다.
$$ \Omega = 4 \cdot \arcsin\left(\sin\left(\frac{\theta}{2}\right) \cdot \sin\left(\frac{\phi}{2}\right)\right) $$- Ω : 입체각 (sr)
- θ : 수평 화각 (radian)
- ϕ : 수직 화각 (radian)
⚠️ 계산 시, 각도를 라디안(radian) 단위로 변환해야 합니다.
이 공식은 0°~180° 범위 내에서 유효하며, 180°를 초과하면 중첩 영역을 고려한 별도 보정이 필요합니다.
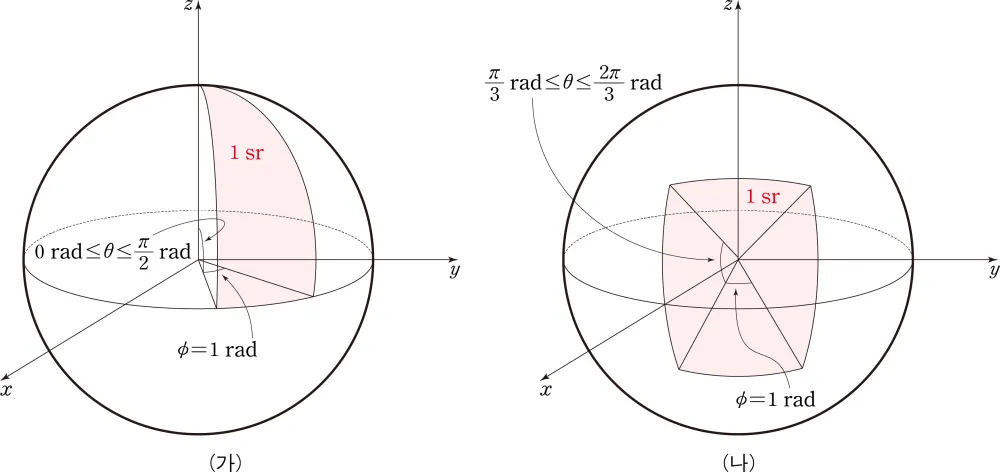
🌐 시뮬레이션으로 보는 입체각의 확장
다음은 화각이 커질수록 입체각이 어떻게 변하는지를 시각적으로 나타낸 예시입니다.
- 🔵 180° × 180° → 반구 시야
- 🟢 190° × 190° → 후방 일부 포함
- 🔴 210° × 210° → 거의 전방위
시야가 넓어질수록 구면 위의 면적이 커지며, 결과적으로 더 넓은 공간을 포괄하게 됩니다.
즉, 카메라나 센서의 화각이 커질수록 입체각 값도 커지는 구조입니다.
🧪 실무에서 유용한 입체각 시뮬레이션 도구
입체각은 직접 계산하기 까다롭기 때문에, 아래와 같은 도구를 활용하면 효율적으로 이해할 수 있습니다.
- Don Hatch’s Solid Angle Calculator
→ 벡터나 삼각형을 기반으로 정확한 입체각 계산 가능 - GeoGebra 3D Graphing
→ 구면 위 시야 모델링 가능, 수평·수직 화각 직접 입력 - Paul Bourke’s Geometry Resources
→ 입체각 수식 및 실무 예제 정리 (광학/위성 분야 활용)
📊 입체각 계산용 엑셀 시트 (활용 팁)
직접 실무에서 사용하기 위해서는 Excel 계산 시트를 만들어 두면 편리합니다.
예를 들어, 100°부터 240°까지의 수평/수직 화각을 입력하면 자동으로 스테라디안 값을 계산하도록 구성할 수 있습니다.
이렇게 하면 렌즈 설계, 조명 배광 설계, 센서 커버리지 계산 등에서 빠르게 결과를 도출할 수 있습니다.
✅ 마무리 요약
| 구분 | 평면각 | 입체각 |
|---|---|---|
| 차원 | 2D | 3D |
| 단위 | 라디안(rad) | 스테라디안(sr) |
| 예시 | 삼각형 내각, 부채꼴 | 카메라 시야, 조명 조사각 |
| 최대값 | 2π rad (360°) | 4π sr (구 전체) |
입체각은 단순히 수학적인 개념이 아니라, 3차원 공간에서의 시야를 다루는 기본 언어입니다.
조명 설계, 카메라 화각, 드론 탐지, 위성 촬영, AR/VR 시야 제한 등—광학 분야의 거의 모든 계산에서 입체각은 핵심 역할을 합니다.
이 글을 통해 평면의 한계를 넘어, 공간을 바라보는 새로운 관점을 얻으셨길 바랍니다. 🌏✨